1. 문제
https://www.acmicpc.net/problem/31003

문제를 요약하면 인접한 수가 서로소인경우 위치 변경을 할 수 있고, 이러한 시행을 무한히 할 수 있을때, 사전순으로 가장 낮은 수열을 출력해야한다.
2. 접근
이 문제의 경우 접근이 상당히 어려운 문제이다. 일단 시간복잡도를 생각해보자. 두 숫자의 서로소관계를 파악하기 위해서는 유클리드 호제법을 사용할 수 있다. 시간복잡도 $O(log(N))$
이러한 시행을 무한히 할 수 있지만, $O(N^2)$ 번의 시행으로 최적의 수열을 만들 수 있다는 것을 어느정도 유추할 수 있다.(직관)
그리디하게 문제를 풀 수 없을까 고민해 봤는데 그리디만으로는 힘들어 보인다.
수열문제를 가끔식 그래프로 푸는 경우가 있는데, 그래프로도 접근해보자
한가지 생각해볼 것은 수열을 만드는중 자리가 정해진 수열은 위치가 변동되지 않는다.(직관)
서로소 관계가 아닌 숫자쌍에 대해서는 해당 숫자의 위치관계가 변하지 않는다.
예제를 직접 해보면 알 수 있다.
위치관계가 변하지 않는다는 특징을 이용해서 각각의 숫자쌍의 관계를 간선으로 표현할 수 있다.
위상정렬과 유사한 형태가 된다.
3. 풀이
예제를 위상정렬의 형태로 표현해보자.
서로소 관계가 아닌 경우(위치관계가 생기는 경우), 간선을 만든다.


숫자는 $7, 3, 4, 2, 6$ 으로 총 5개 이다.
앞에서 부터 서로소 관계를 파악해보자
$7$의 경우 첫번째 숫자이기 때문에 skip한다.

$3$의 경우 앞의 $7$과 서로소 관계 이기 때문에 간선을 만들지 않는다.

$4$역시 $3,7$와 서로소 관계 이기 때문에 간선을 만들지 않는다.

$2$의 경우 $4$와 서로소 관계가 아니기 때문에 간선이 생긴다.
$2$가 $4$보다 선행될 수 없음을 의미한다.

$6$의 경우에 $3,4,2$ 와 서로소 관계가 아니므로 간선이 생긴다.
이제 수열을 만들어보자.
사전 순으로 가장 작은 수열을 만들기 때문에 가장 작은 값 부터 넣어야한다.

가장 작은 숫자가 2이지만 2는 위치관계가 존재하여 4가 선행되어야 한다.
두번째로 작은 숫자인 3을 보자 3은 다른 위치관계(3을 가리키는)가 존재하지 않아 사용할 수 있다.

3을 사용하고 3이 가리키는 간선을 삭제한다.(3이 선행된 위치관계를 만족하기 때문에)
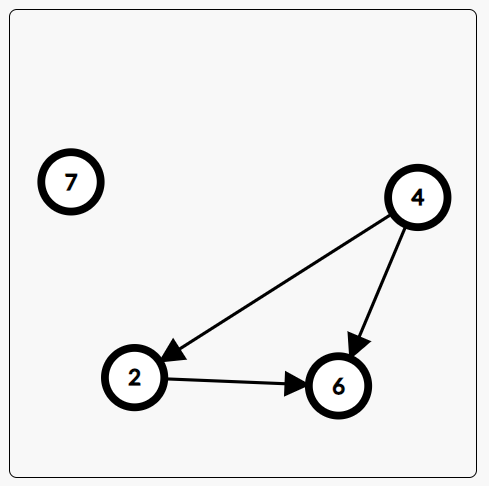
2는 여전히 사용 불가능하다.
두번째로 큰 4는 사용할 수 있다.
4를 사용하고 4이 가리키는 간선을 삭제한다.


이제 2를 사용할 수 있다.
2를 사용하면 모든 간선이 삭제되어 나머지 숫자들도 작은 순서대로 넣을 수 있게된다.

문제에 대한 해결방법은 파악했는데 몇가지 생각해야 하는 것이 더 있다.
정렬되어 있는 그래프에 대해서 접근할 수 있어야 한다.
우선순위 큐를 사용한다.
또한 예제의 경우 두번째 값에서 모두 처리되었지만, N번째에서 처리된다는 점에서 1부터 N-1까지의 그래프 정보를 가지고 있어야한다.
글쓴이는 스택을 사용하여 그래프 정보를 기억했다.
따라서 매번 step마다
- 우선순위 큐의 top이 연결관계가 없는지 파악한다.
- 연결관계가 있다면 스택에 저장하고 1로 이동한다. 연결관계가 없다면 3으로 이동한다.
- 결과 배열에 추가하여 해당 노드가 가리키는 간선을 지운다.(indegree 배열로 처리)
- 스택에 있는 모든 값을 우선순위 큐에 push 한다.
- 스택이 비어있지 않다면 1번부터 진행
시간 복잡도는 $O(N^2)$이다.
따라서 전체 시간 복잡도는 그래프 생성+그래프 처리 으로 $O(N^2(log(N+1))$ ->$O(N^2(log(N)$이다.
4. 코드
#include <bits/stdc++.h>
using namespace std;
int N;
int arr[3001];
vector<int> vec[3001];
int inDegree[3001] = {0};
struct compare{
bool operator()(pair<int,int>pair1,pair<int,int>pair2){
return pair1.first>pair2.first;
}
};
priority_queue<pair<int,int>,vector<pair<int,int>>,compare>pq;
stack<pair<int,int>>stk;
vector<int>result;
void cal(){
while(!pq.empty()){
pair<int,int>pair1;
while(1){
pair1=pq.top();
pq.pop();
if(inDegree[pair1.second]==0)
break;
stk.push(pair1);
}
result.push_back(pair1.first);
for(int i=0;i<vec[pair1.second].size();i++){
int num=vec[pair1.second][i];
inDegree[num]--;
}
while(!stk.empty()){
pq.push(stk.top());
stk.pop();
}
}
}
int main() {
cin.tie(NULL);
ios::sync_with_stdio(false);
cin >> N;
for (int i = 1; i <= N; i++) {
cin >> arr[i];
pq.push({arr[i],i});
}
for (int i = 1; i <= N; i++) {
for (int j = i + 1; j <= N; j++) {
if (gcd(arr[i], arr[j]) != 1) {
vec[i].push_back(j);
inDegree[j]++;
}
}
}
cal();
for(int i=0;i<result.size();i++){
cout<<result[i]<<" ";
}
}'PS > 백준' 카테고리의 다른 글
| [백준 10973번] 이전 순열 C++ 풀이 (1) | 2024.02.07 |
|---|---|
| [백준 28437번] 막대 만들기 C++ 풀이 (0) | 2023.08.07 |
| [백준 26113번] Two Choreographies C++ 풀이 (3) | 2023.07.30 |
| [백준 24553번] 팰린드롬 게임 C++ 풀이 (1) | 2023.07.06 |
| [백준 28283번] 해킹 C++ 풀이 (0) | 2023.07.03 |
