스터디중 LCA공부중 첼린지 문제를 정하고 공부하면 좋을 것 같아, ICPC문제길래 선택했던 문제인데, 푸는데 걸린 시간이 가장 오래걸린 문제로 거이 4개월이 걸렸다. (심지어 풀이는 LCA를 쓰지 않았다..)
1.문제
https://www.acmicpc.net/problem/26113
26113번: Two Choreographies
Your program is to read from standard input. The input starts with a line containing a single integer, $n$ ($4 ≤ n ≤ 100\,000$), where $n$ is the number of static motions two dancers can represent. Each static motion is numbered as an integer from $1$
www.acmicpc.net

https://www.notion.so/Two-Choreographies-1f534136543c4105b5b1451fe88a9c0a?pvs=4
지문이 영어라 영어를 못하는 나같은 사람들을 위해 만든 번역본을 위 노션 링크로 확인 할 수 있다.
문제를 요약하면 $n$ 개의 간선에서 대해서 $2n-3$ 개의 무방향 간선 정보에 대해서 동일한 길이의 사이클을 찾을 수 있다면 해당 사이클 두개 각각의 노드들을 출력하고 동일한 길이의 사이클을 찾을 수 없다면, $-1$을 출력해야한다.
2. 접근
1. dfs, bfs
사이클을 찾는 방법을 떠올려보자.
아주 basic한 방식은 dfs 를 하면서 back edge라면 사이클이다.
그러나 이방법을 사용하는 것은 꽤나 힘들어 보이는데, 모든 사이클을 찾기에 한계가 있기 때문이다.
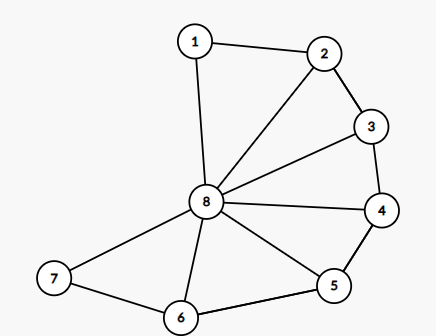
만약 위와 같은 그래프가 주어 졌다면 back edge를 만났을때, 사이클의 길이를 결정하기 힘들어 보인다.
예를 들어 $ 1 2 3 4 8 1$ 으로 탐색하였을때 우리가 사이클의 길이를 무작정 사이에 있는 노드 수로 결정한다면 $5$일텐데, $5$이외에도 $8 1$로 만들어지는 사이클의 길이가 다양하기 때문에 사이클을 찾을 수 도 없을 것 같다고 판단했다.
그러면 bfs를 사용한다면?
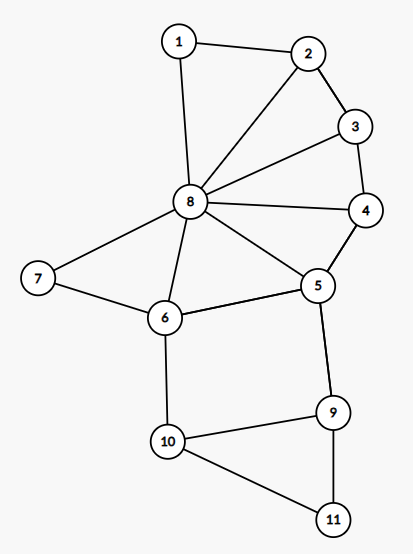
bfs의 경우에도 위와 같이 노드를 추가한 상태에서 $8$번 노드부터 탐색을 시작한다고 생각하면 모든 사이클을 찾을 수 없다.
2. 다른 방법
사이클을 찾을 수 있는 다른 방법을 생각해보자.
SCC: 방향 그래프에서 사이클을 찾는데 사용할 수 있긴 하네 무방향 그래프도 간선이 2개라고 생각하고 접근해보자. -> SCC도 모든 사이클을 찾을 수 없다.
LCA: 사이클을 찾는데 쓸 수 있을까?
조금만 생각해도 여러 반례가 떠올라서 아에 배제하였다.
3. 간선의 개수
간선의 개수가 $2n-3$ 개이다. 여러 예제를 가지고 흔히 노다가를 해보면 $2n-3$ 개의 간선이 존재하면 많은 사이클이 만들어짐을 확인 할 수 있다.
mst가 $n-1$ 이기 때문에 남은 간선 $n-2$개가 추가 될 때 마다 사이클이 반드시 만들어진다.
나올수 있는 사이클의 길이가 $ 3 \leq cycle_{len} \leq n$ 이기 때문에 $n-2$가지의 사이클 길이가 존재한다.
그런데 사이클이 $n-2$개 더 만들어지기 때문에 동일한 길이의 사이클 2개가 거이 대부분 만들어질수 있다는 추측을 해볼수 있다.
따라서 모든 다른 길이의 사이클이 존재한다면 그때를 제외하고 반드시 사이클 2개를 찾을 수 있다.
4. 비둘기집의 원리
위의 정보를 바탕으로 코드를 짜봤는데 계속 틀렸다.
내가 간과한 정보가 하나 있었는데 남은 간선 $n-2$개가 추가 될 때 마다 사이클이 반드시 만들어질때, 하나만 생기는 경우는 mst 직후이고, 이후에는 간선이 하나 추가 될때마다 이미 사이클이 존재한 그래프에 간선을 추가한 것이기 때문에 새로운 사이클이 2개이상 생길 수 있다.
증명은 하지 못했는데 아래 그림과 같이 직관을 활용했다.
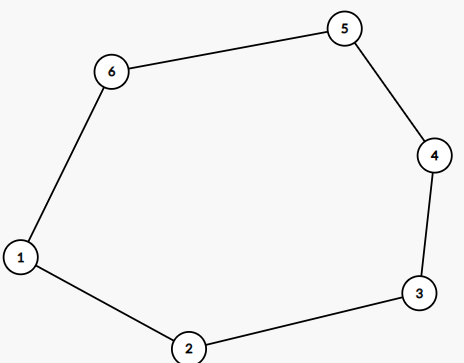
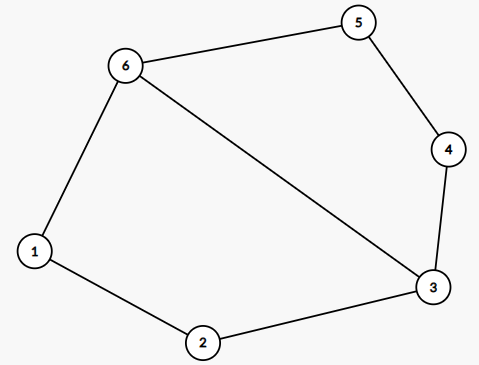
따라서 모든 다른 길이의 사이클이 존재하는 경우에도 반드시 동일한 길이의 사이클을 찾을 수 있겠다 라고 생각했다.(이 생각을 떠올리는데 거진 1개월을 사용했다.)
5. 사이클 찾기
그러면 어떻게 찾을 수 있을까?
이부분이 가장 어렵다고 느꼈는데 확실하게 사이클을 찾는 방법이 존재했다.
먼저 위에서 이야기 했던 dfs를 통해 탐색하면서 사이클을 찾아낸다.
그러면 사이클을 전부 찾을 수 없는데???
만약 사이클을 전부 찾을 수 없어서 동일한 길이의 사이클을 찾지 못한경우가 존재하면 그경우는 내가 찾은 사이클이 모두 길이가 달라야한다. 따라서 모두 길이가 다른 사이클에서 아직 찾지 못한 사이클을 하나만 찾으면 되는데, 가장 길이가 긴 사이클 $cycle_a$ 을 생각 해보자.
$cycle_a$는 어떤 경우에도 우리가 형태를 알 수 있다.(모든 노드를 탐방하기 때문에)
그러면 $cycle_a$ 보다 길이가 $1$ 짧은 $cycle_b$를 생각해보자
$cycle_b$는 $cycle_a$ 에서 노드하나를 뺀것이다.
이때 뺀 노드를 $node_a$라고 하고, $node_a$의 양옆 노드를 $node_b$, $node_c$라고 한다면 $node_b$와$node_c$를 잊는 간선이 반드시 존재한다.
그런데 $node_a$와$node_c$ 사이에 간선이 존재하고, $node_a$와$node_b$ 사이에 간선이 존재하기 때문에(가장 긴 사이클의 구성요소) $node_a$, $node_b$$node_c$를 이어 길이가 3인 사이클을 만들 수 있고, 이 사이클은 아직 우리가 찾은 사이클이 아님이 보장된다. (만약 이미 찾았으면 $cycle_b$를 찾지 못해 모순이므로 귀류법을 통해 증명)
사이클을 경로는 어떻게 구할 수 있을까?
이전 경로를 저장하는 back arr를 통해 재귀적으로 추적 가능하다.
3. 구현
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
vector<int>vec[100001];
int back[100001];
int visited[100001] = { 0 };
int visited2[100001] = { 0 };
vector<pair<int, int>>cycle[100001];//첫번째는 가장끝 두번째는 첫번째 노드 끝에서 back으로 오면됨
int N;
void printnode(pair<int, int>node) {
int end = node.first;
int start = node.second;
while (1) {
cout << end << " ";
if (end == start)
break;
end = back[end];
}
cout << "\n";
return;
}
void dfs(int node, int prenode, int index) {
if (visited[node] != 0) {//사이클 발생
if (visited[prenode] - visited[node] + 1 >= 3) {
cycle[visited[prenode] - visited[node] + 1].push_back({ prenode,node });
}
return;
}
visited[node] = index;
back[node] = prenode;
for (int i = 0; i < vec[node].size(); i++) {
dfs(vec[node][i], node, index + 1);
}
return;
}
int main() {
cin.tie(NULL);
ios::sync_with_stdio(false);
int temp1, temp2;
cin >> N;
for (int i = 1; i <= (2 * N) - 3; i++) {
cin >> temp1 >> temp2;
vec[temp1].push_back(temp2);
vec[temp2].push_back(temp1);
}
for (int i = 1; i <= N; i++) {
if (visited[i] != 0)
continue;
dfs(i, 0, 1);
}
bool istrue = false;
for (int i = 3; i <= N; i++) {
if (cycle[i].size() >= 2) {
cout << i << "\n";
printnode(cycle[i][0]);
printnode(cycle[i][1]);
istrue = true;
break;
}
}
if (!istrue) {
cout << 3 << "\n";
printnode(cycle[3][0]);
vector<int>vec6;
vec6.push_back(cycle[N][0].first);
vec6.push_back(cycle[N][0].second);
vec6.push_back(cycle[N - 1][0].first);
vec6.push_back(cycle[N - 1][0].second);
sort(vec6.begin(), vec6.end());
unique(vec6.begin(), vec6.end());
for (int i = 0; i < 3; i++)
cout << vec6[i] << " ";
}
return 0;
}'PS > 백준' 카테고리의 다른 글
| [백준 10973번] 이전 순열 C++ 풀이 (1) | 2024.02.07 |
|---|---|
| [백준 28437번] 막대 만들기 C++ 풀이 (0) | 2023.08.07 |
| [백준 24553번] 팰린드롬 게임 C++ 풀이 (1) | 2023.07.06 |
| [백준 28283번] 해킹 C++ 풀이 (0) | 2023.07.03 |
| [백준 28305번] 세미나 배정 C++ 풀이 (1) | 2023.07.02 |
