이 블로그는 개인의 공부 목적으로 작성된 블로그입니다. 왜곡된 정보가 포함되어 있을 수 있습니다
1. 등장배경
대칭키 암호화 방식에는 키가 노출되었을때 암호화 복호화를 누구나 할 수 있는 치명적인 단점이 존재
디피와 헬만이 암호화 키를 안전하게 공유하기 위해서 비대칭키를 사용하는 방법을 떠올리게 됨(Diffie-Hellman key exchange Protocol)
https://ko.wikipedia.org/wiki/%EB%94%94%ED%94%BC-%ED%97%AC%EB%A8%BC_%ED%82%A4_%EA%B5%90%ED%99%98
디피-헬먼 키 교환 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 디피-헬먼 키 교환(Diffie–Hellman key exchange)은 암호 키를 교환하는 하나의 방법으로, 두 사람이 암호화되지 않은 통신망을 통해 공통의 비밀 키를 공유할 수 있도
ko.wikipedia.org
이때 등장한 비대칭키를 활용하여 공개키 암호화 방식및 전자서명등 다양한 보안 프로토콜이 생성되었다.
2. 정수론
비대칭키는 정수론의 기반한 수학적인 방법으로 암호화한다. 필요한 정수론 지식을 학습해보자(두서 없이 개념이 등장할 계획인데 결국 오일러정리와 페르마의 소정리를 위한 것이기 때문에 이해가 안된다면 흐름을 보는 것을 추천)
1.Group
집합 $(S,\bigoplus)$ 에 대하여 집합 $S$에 대해 다음 조건을 모두 만족하면 집합 $S$가 연산 $\bigoplus$에 대해 집합이 Group이다.
1. Closure: $\forall$a,b we have $a \bigoplus b \in S$ (해당 연산에 대해서 닫혀있다.)
2. Identity: $\exists$ an $ e \in S$ s,t $e \bigoplus a = a \bigoplus e =a$, $\forall a \in S$ (항등원이 존재한다)
3. Associativity: $ \forall a,b,c \in S $ , $ (a\bigoplus b) \bigoplus c= a\bigoplus (b \bigoplus c)$ (결합법칙이 성립한다)
4. Inverse: For each $a \in S$, $\exists $unique element $b\in S$ s.t. $a \bigoplus b= b \bigoplus a =e$ (역원이 존재한다.)
또한 $S' \subseteq S$인 $S'$에 대해서 $(S',\bigoplus)$ 도 group일경우 $S'$를 $S$의 Subgroups이라고 한다.
2. Abelian Group
group $(S,\bigoplus)$ 가 commutative law를 만족하는 경우 Abelian Group이다.
commutatuve law: $a \bigoplus b =b \bigoplus a \forall a, b \in S$
3. Finite Group
$|S|=n$ 인 경우 Finite Group 이다.(원소의 갯수가 유한개인 경우)
4. equivalence class
$n$으로 모듈러 연산을 수행했을때, $a$을 가지는 집합을$[a]_n$이라고할때,
$[a]_n=\{a+kn | k\in Z \}$ 이다
$Z_n=\{[a]_n| 0\le a \le n-1 \}$ 이라고 정의하면
$Z_n=\{ 0,1,..,n-1 \}$
$Z^*_n=\{[a]_n \in Z_n | gcd(a,n)=1 \}$ 으로 정의($gcd(a,n)$은 최대 공약수 따라서 서로소를 가리킴)
5. 관찰
$a \equiv a' (mod n) $이고 $b \equiv b'(mod n)$ 인경우,
1) $a+b \equiv a'+b'(mod\ n)$
2) $ab \equiv a'b' (mod n)$ (증명 생략)
따라서 다음과 같이 표현할수 있다
$[a]_n+_n [b]_n =[a+b]_{n'}$
$[a]_n ._n [b]_n=[ab]_n$ (이때 $+_n, ._n$은 각각 덧셈 곱셈 연산후 모듈러연산 진행)
이때 $Z_n$ 은 $+n$에 대해서 finite abelian group를 만족하고 $(Z_n,+_n)$
$Z^*_n$은 $._n$ 에 대해서 finite abelian group을 만족 $(Z^*_n, \ ._n)$ ( $Z_n$의경우 $0$에서 역원을 만들어 내지 못함)
6. $Z^*_n , \ ._n$ 에서의 역원 구하기
$(Z^*_n, \ ._n)$가 finite abelian group이기 위해서는 역원이 존재해야함
이때 항등원은 $1$ (곱셈 결과가 1이되므로)
따라서 $Z^*_n$의 모든 원소에 대해서 $A . \_n B=1$ 을 만족하는 $A\ B$를 찾아야한다 $A,B \in Z^*$
ex) $n=10$ 인경우 $Z^*_n=\{ 1,2,4,7,8,11,13,14 \}$
| $Z^*_{15}$ | 1 | 2 | 4 | 7 | 8 | 11 | 13 | 14 |
| 1 | 1 | 2 | 4 | 7 | 8 | 11 | 13 | 14 |
| 2 | 2 | 4 | 8 | 14 | 1 | 7 | 11 | 13 |
| 4 | 4 | 8 | 1 | 13 | 2 | 14 | 7 | 11 |
| 7 | 7 | 14 | 13 | 4 | 11 | 2 | 1 | 8 |
| 8 | 8 | 1 | 2 | 11 | 4 | 13 | 14 | 7 |
| 11 | 11 | 7 | 14 | 2 | 13 | 1 | 8 | 4 |
| 13 | 13 | 11 | 7 | 1 | 14 | 8 | 4 | 22 |
| 14 | 14 | 13 | 11 | 8 | 7 | 4 | 2 | 1 |
$1$을 가지는 $A\ B$ 순서쌍이 모든 원소에 대해 존재함을 확인가능
7. Euler's phi function
그러면 $Z^*_n$의 갯수를 셀수 있을까?
https://en.wikipedia.org/wiki/Euler%27s_totient_function
Euler's totient function - Wikipedia
From Wikipedia, the free encyclopedia Number of integers coprime to and not exceeding n "φ(n)" redirects here. For other uses, see Phi. Not to be confused with Euler function. The first thousand values of φ(n). The points on the top line represent φ(p)
en.wikipedia.org
$|Z^*_n|= \varphi(n)$ , $\varphi=n\prod_{p|n}^{}(1-\frac{1}{p})$ ($p$는 $n$의 약수 이면서 prime number)
이때 $p$가 prime number의 경우 $\varphi(p)=p-1$
8. generate, order
$(S,\bigoplus)$ 에 대해서 $a \in S$ 인 $a$값에 대해서 $a^{(k)}=a \bigoplus a \bigoplus a \bigoplus .. \bigoplus a$
일때 $<a>=\{ a^{(k)} | k \geq 1 \}$ 으로 subgroup $<a>$ 를 정의한다(무조건 성립하지 않는것 같다 group 조건을 만족하지 않을 수 있기때문에)
만약 $a^{(t)}=e$일 경우 $ord(a)=k$ 라고한다.
또한 $ ord_n(g)=|Z^*_n|$ 인경우를 primitive root, generator 라고 한다.또한 primitive root를 가지는 $Z^*_n$을 cyclic하고 표현한다.
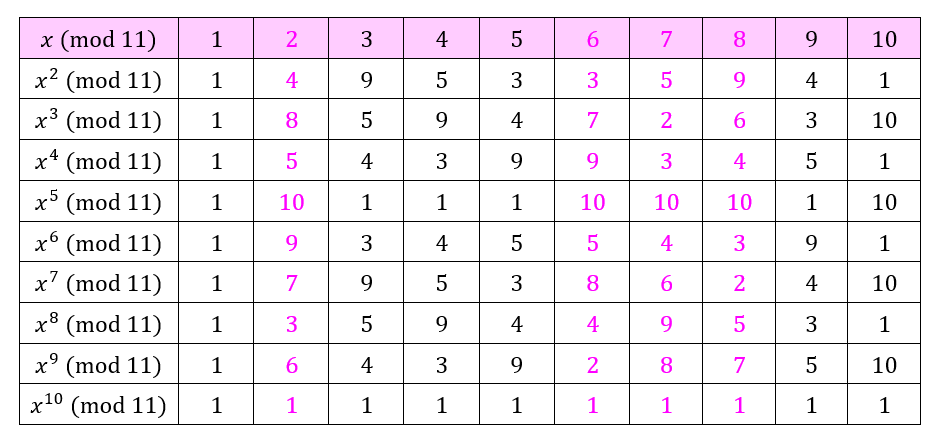
$Z_{11}^*$ 의경우 $2,6,7,8$ 라는 generator를 가진다.
이때 우리는 $|Z_n^*|$만큼 연산을 하는 것을 확인할수 있음(위의경우 $10$)
또한 $|Z_n^*|$ 만큼 연산한 값에 대해서 $1$ 이 되는 것을 확인 할 수 있다.$(a\in Z_n^*; \ \ \ a^{|Z^*_n|=1})$
3. Euler's Theorem
$n>1$인 모든 정수에 대해서 $a^{\phi} \equiv 1\ (mod \ n$이고 이때, $a\in Z^*_n$
4. Fermat's Little Theorem
$a^{p-1}\equiv 1 (mod \ p) $이고 이때 $a\in Z^*_p$
3,4 이 대칭키 암호화 알고리즘을 사용하기 위한 핵심 특징
'보안' 카테고리의 다른 글
| [Spring Security in action] 스프링 시큐리티 시작하기 (0) | 2024.01.11 |
|---|---|
| [보안] 전자 지불 시스템, 전자 화페 (0) | 2023.12.08 |
| [보안] 전자서명 (0) | 2023.12.02 |
| [보안] 비대칭 암호화, ElGamal, RSA (3) | 2023.12.01 |
| [보안] 대칭키 와 DES 알고리즘3 (0) | 2023.11.30 |
