이 블로그는 개인의 공부 목적으로 작성된 블로그입니다. 왜곡된 정보가 포함되어 있을 수 있습니다
1. 대칭키
암호화에 필요한 키를 양쪽 모두 동일한 키를 사용하는 방식
이때 해당하는 키를 비밀키라고도 부른다.
대칭키, 비밀키, 공유키, 개인키, 공개키 등 여러암호화 단어가 헷갈린다면 천천히 생각해보자
대칭키는 이름에서 말하듯 키를 대칭하여 같이 쓰겠다는 것이다.
그러면 해당키가 외부로 노출된다면 어떻게 될까?
$ \to $ 누구나 암호화 할 수 있고, 누구나 복호화 할 수 있다.
키가 절대 노출되어선 안된다. 따라서 우리는 이때의 키를 비밀키라고 부를 수 있다.
2. 암호학적 강도
대칭키에서는 해당 암호화방식의 강도를 혼돈과 확산이라는 2가지 키워드로 측정할 수 있다.
혼돈: 암호문의 통계적 성질과 원문의 통계적 성질의 유사도이다. 높을 수록 암호가 난해하다고 할 수 있고, 빈도분석 방법으로 해독하기 어려워진다.
확산: 암호문에서의 비트차이와 원문에서의 비트차이(이것도 통계적 특징 아닌가?), 높을 수록 암호가 난해하다고 할 수 있다.
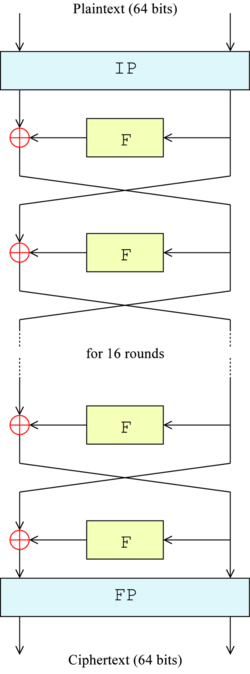
3. DES 암호화 알고리즘
대칭키 알고리즘을 사용한 암호화 방법중 하나
64비트의 단위 기준으로 (블럭이라고 정의) 16번 암호화
이때 매 암호화 마다 블럭 교환이 일어난다.
암호화키는 56비트(8비트 마다 parity bit가 추가됨)
4. CBC
이전암호화 결과가 이후에 발생하는 암호화에 영향을 주는 방식
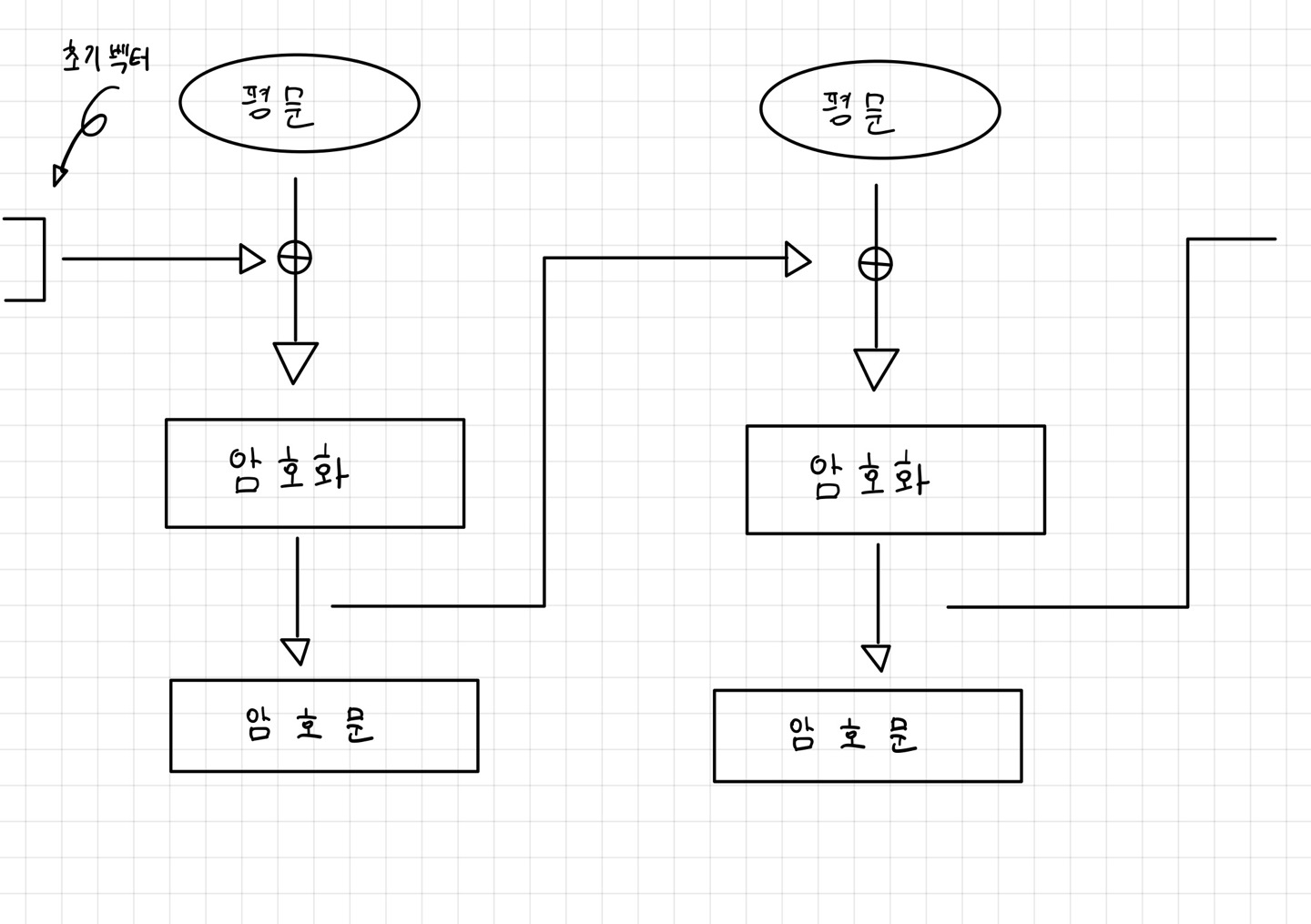
이전에 암호화 했던 값과 평문을 합쳐서 암호화한다.
처음에는 초기벡터를 활용하여 진행한다.
이때 $xor$ 함수를 사용할 경우 복호화를 쉽게 처리할 수 있음 (암호문을 복호화 한 값과 앞 block의 암호화값을 $xor$ 한값)
CBC 방식을 사용할 경우 같은 평문에 대해서 다르게 암호화결과가 나올 수 있다.
이때 des알고리즘은 암호화후 해당값을 중간기준으로 교차시켜 $64bit$ 를 $32bit$, $32bit$ 로 쪼갬 다음 암호화에 사용
5. 비트확장
$32bit$ 을 $48bit$로 확장해줘야 하는데(s-box를 사용하기 위해서 그런것으로 추정) $4bit$씩 8개로 쪼개여 각각의 $4bit+양옆bit$를 더해 $6*8=48bit$로 확장
6. S-BOX, P-BOX
대칭키의 암호학적 강도인 혼돈과 확산을 증가시키기 위한 방법으로 데이터의 불규칙성을 증가시키는 일종의 치환 상자.
s-box

input을 들어오는 $48bit$ 에 대해서 $6bit$ 씩 쪼개여 최상위 비트와 최하위 비트를 짝지어 Outer bits을 생성하고, 나머지 4bit로 표에 해당하는 4비트 값으로 치환 (위의 경우 011011->(01, 1101)
p-box
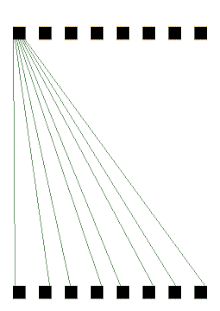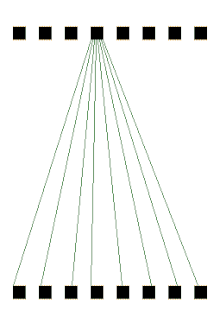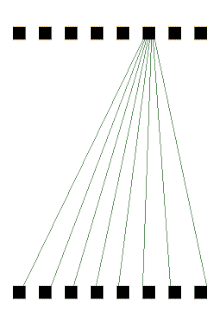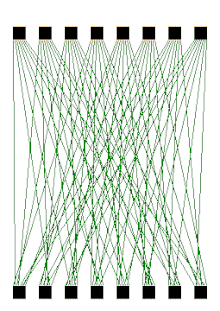
input으로 들어오는 32bit에 대해서 순서를 해당 p-box에 표시된것으로 sort
7. 정리

1. input으로 들어온 $64bit$를 $32bit$ 씩 L,R로 구분
2. R에 대해서 비트확장 ($32bit \to 64bit$)
3. key값에 대해서 56bit에 대해서 shift 연산과 압축연산을 통해 적절한 $48bit$의 block 키값 형성 하여 2.와 $xor$연산 $(F(R_{i-1},K_i))$
4. S-BOX 로 비트 치환
5. P-BOX 로 비트 변환
6. L값과 5.값을 $xor$ $(R_i=L{i-1} \bigoplus F(R_{i-1},K_i))$
7. R값은 연산전 L값 $(L_i=R_{i-1})$
8. DES의 한계
DES는 결국 S-BOX의 의존하기 때문에 8개의 S-BOX를 사용했지만 복호화를 성공한 사례가 발생
경우의 수가$2^{56}$ 으로 브루트포스 가능
트리플 DES
기존의 $56bit$의 키 대신$112bit$의 키를 사용(2배길이)하는 암호화 알고리즘
$112bit$를 2개의 $56bit$ 키$k1$ $k2$로 나누어 암호화 $\to$ 복호화 $\to$암호화 순으로 진행
$C1=E(P,K1)$
$C2=D(C1,K2)$
$C1=E(C2,K1)$
번외) 더블 DES의 경우 평문과 암호문이 노출될경우 양쪽에서 암복호화를 하는경우, $2^{56+1}$ 만큼의 연산으로 찾는것이 보장되기 때문에 사용하지 않는다고 한다
'보안' 카테고리의 다른 글
| [Spring Security in action] 스프링 시큐리티 시작하기 (0) | 2024.01.11 |
|---|---|
| [보안] 전자 지불 시스템, 전자 화페 (0) | 2023.12.08 |
| [보안] 전자서명 (0) | 2023.12.02 |
| [보안] 비대칭 암호화, ElGamal, RSA (3) | 2023.12.01 |
| [보안] 공개키와 비대칭 암호화 알고리즘 (1) | 2023.11.30 |
