이 블로그는 개인의 공부 목적으로 작성된 블로그입니다. 왜곡된 정보가 포함되어 있을 수 있습니다
0. beginning
몇년전, 알파고 부터 시작해서, 올해는 OpenAi의 ChatGPT와 같은 AI가 주목을 받고 있다. 현재 대부분의 AI기술은 Deep learning 기술을 활용하고 있다. 이번 시간에 Deep learning 기술의 근간이 되는 Artificial Neural Network에 대해 알아보고 이해해보자.(Artificial Neural Network, Deep Neural Network, DNN 모두 동일한 의미로 사용되는 것 같다.
1. 퍼셉트론
Neural Network를 이해하기전에 먼저 Neural Network의 기원인 퍼셉트론의 대해서 생각해보자
퍼셉트론을 다수의 신호를 입력으로 받아 하나의 신호를 출력하는 것이다. 아래 사진은 퍼셉트론의 예시이다.
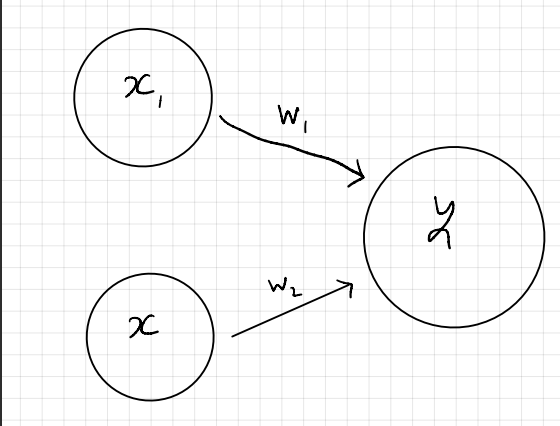
$x_1$ $x_2$ 는 신호이고 각각 $w_1$ $w_2$라는 가중치가 곱해져서 $y$ 라는 신호를 생성한다. 이때 $y$ 값은 일정 범위를 넘어쓰면 $1$ 을 출력 그렇지않으면 $0$을 출력한다. 이러한 퍼셉트론을 활용하여 다양한 분류문제를 해결할 수 있다.
그러나 퍼셉트론의 문제는 한계가 존재하는데, XOR와 같은 문제를 해결하지 못한다는 것이다. 결국 퍼셉트론을 만드는 것은 선형함수를 만드는것과 동치인데, XOR 와 같은 경우 선형함수로는 해결할 수가 없기 때문이다.
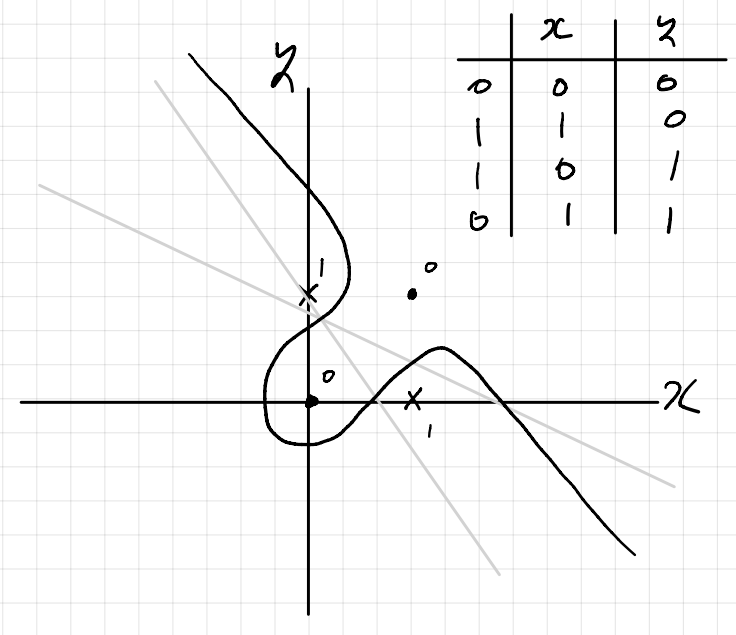
그러면 어떻게 하면 비선형 함수를 표현할수 있을까?
2. 다층 퍼셉트론
여러 층을 쌓아서 퍼셉트론을 만든다면 해결할 수 있다!
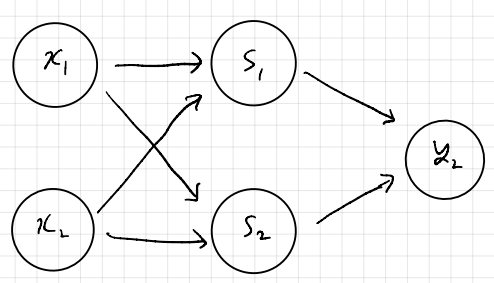
자세한 과정을 생략하겠다. 약간 설명을 덧붙이면 하나의 층으로 만드는 퍼셉트론에서 AND, OR 을 구현 할 수 있는데, 이러면 AND, OR을 조합하여 XOR을 만들 수 있기 때문에 같은 맥략해서 다층 퍼셉트론을 사용하면 XOR문제를 해결할 수 있다는 것이다. 이때 우리가 주목해야하는 점은 각각의 층 또는 노드들이 AND, OR와 같이 하나의 역활을 한다는 것이다. 이것을 확장해보면 다층 퍼셉트론을 활용하여 다양한 문제를 해결할수 있다는 추측을 할 수 있게 된다.
3. 신경망(Neural Network)
신경망은 퍼셉트론와 동일한 형태를 가진다. 일반적으로 입력층, 은닉층, 출력층 이렇게 3개로 노드를 분류한다.
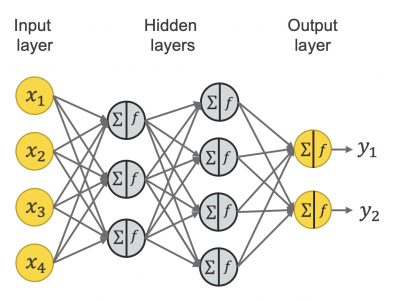
그러면 신경망과 퍼셉트론의 차이점이 무엇인가라고 생각해본다면 신경망은 활성화함수를 사용한다.
기존의 퍼셉트론은 나온값이 기준치에 따라 0,1중 하나의 값(계단함수라고 부른다)을 사용했다면 신경망은 더양한 활성화함수를 사용한다.
4. 시그모이드 함수(Sigmoid function)
$h(x)=\frac{1}{1+exp(-x)}$
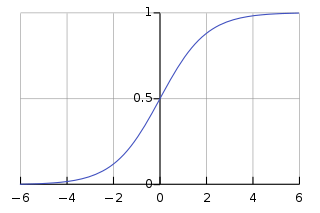
시그모이드 함수를 사용하는경우, 기존 계단함수와 달리 입력에 따라 출력이 연속적으로 변화하고 항상 출력이 0과 1 사이의 값이다. 이러한 시그모이드 함수를 활성화 함수로 사용하게 되면, 기존의 신경망안의 은닉층에서 값들이 버려지지 않고, 신경망이 알수 있도록 연속적인 값들을 반환해준다는 점에서 이점이 있는 것이다!
5. 손실 함수(loss function)
그러면 이러한 신경망을 어떻게 개선할 것인가?(인공지능에서는 학습이라고 한다) 개선하기 위해서는 나온 결과가 옳바른 판단을 했는지에 관한 판단기준이 필요하다. 우리는 원래의 정답과 예측한 값을 손실함수를 정의하여 손실함수를 최소화하도록 가중치의 값을 조정할 생각이다. 손실함수는 다양한 방식으로 측정되는데, 우리는 binary cross entropy을 손실함수로 사용한다. cross entropy은 다음과 같이 정의한다.
$D(S,L)=- \sum_{}^{i}L_ilog(S_i)$
(binary cross entropy를 사용하는 경우 분류기준이 2개 이상인 Multinomial Classification 문제를 해결하지 못함)
6. 소프트 맥스 함수(softmax function)
$S(y_i)=\frac{e^{y_i}}{ \sum_{}^{j}e^{y_i} }$
분류 문제에 활용되는 활성화 함수이다. 예를 들면 10개의 종류를 분류하는 문제를 생각해보자. 이경우 신경망의 출력층이 10개의 노드로 되어있는데 이때 노드의 값이 클수록 해당 인덱스가 정답일 확률이 높아지게 되는것이다. 이때 확률로 표현하기 위해 모든 출력층 노드의 합을 1로 하기 위해 사용한다.(데이터의 일반화라고 할 수 있겠다.)
7. 비선형문제 ->선형문제
SVM에서 커널트릭으로 비선형 문제를 선형문제로 바꾼것과 동일하게 결국 신경망도 선형문제로 바꿀 수 있다.
8 역전파 알고리즘
$x_{i+1}=x_i-\gamma _i \bigtriangledown f(x_i)$
경사하강법으로 가중치값을 조정해나가는데 이때 만약에 신경망의 은닉층이 매우 많다고 가정해보자
합성함수의 미분법을 생각해보면 $y=f(g(x))$의 형태의 합성함수를 미분하면 $y'=f'(g(x))g'(x)$이다.
따라서 은닉층의 개수가 4개만 있더라도 미분식 $y=f(g_1(g_2(g_3(g_4(x)))))$으로 미분하게 되면 미분의 미분의 미분을 하게된다.... 계산량이 늘어나고 우리가 기억해야하는 변수의 개수도 많아진다.
그러나 역전파 알고리즘을 사용하면 backward를 하면서 앞 노드의 미분값과 가중치 weight와 연산의 형태만 알고 있으면 계속해서 미분을 할 수 있어 효율적이다.
역전파 알고리즘의 자세한 설명은 생략하겠다.
'AI > 기계학습' 카테고리의 다른 글
| [기계학습] CNN(Convolutional Network) (1) | 2023.12.09 |
|---|---|
| [기계학습] Artificial Neural Network 2 (0) | 2023.12.03 |
이 블로그는 개인의 공부 목적으로 작성된 블로그입니다. 왜곡된 정보가 포함되어 있을 수 있습니다
0. beginning
몇년전, 알파고 부터 시작해서, 올해는 OpenAi의 ChatGPT와 같은 AI가 주목을 받고 있다. 현재 대부분의 AI기술은 Deep learning 기술을 활용하고 있다. 이번 시간에 Deep learning 기술의 근간이 되는 Artificial Neural Network에 대해 알아보고 이해해보자.(Artificial Neural Network, Deep Neural Network, DNN 모두 동일한 의미로 사용되는 것 같다.
1. 퍼셉트론
Neural Network를 이해하기전에 먼저 Neural Network의 기원인 퍼셉트론의 대해서 생각해보자
퍼셉트론을 다수의 신호를 입력으로 받아 하나의 신호를 출력하는 것이다. 아래 사진은 퍼셉트론의 예시이다.

$x_1$ $x_2$ 는 신호이고 각각 $w_1$ $w_2$라는 가중치가 곱해져서 $y$ 라는 신호를 생성한다. 이때 $y$ 값은 일정 범위를 넘어쓰면 $1$ 을 출력 그렇지않으면 $0$을 출력한다. 이러한 퍼셉트론을 활용하여 다양한 분류문제를 해결할 수 있다.
그러나 퍼셉트론의 문제는 한계가 존재하는데, XOR와 같은 문제를 해결하지 못한다는 것이다. 결국 퍼셉트론을 만드는 것은 선형함수를 만드는것과 동치인데, XOR 와 같은 경우 선형함수로는 해결할 수가 없기 때문이다.

그러면 어떻게 하면 비선형 함수를 표현할수 있을까?
2. 다층 퍼셉트론
여러 층을 쌓아서 퍼셉트론을 만든다면 해결할 수 있다!

자세한 과정을 생략하겠다. 약간 설명을 덧붙이면 하나의 층으로 만드는 퍼셉트론에서 AND, OR 을 구현 할 수 있는데, 이러면 AND, OR을 조합하여 XOR을 만들 수 있기 때문에 같은 맥략해서 다층 퍼셉트론을 사용하면 XOR문제를 해결할 수 있다는 것이다. 이때 우리가 주목해야하는 점은 각각의 층 또는 노드들이 AND, OR와 같이 하나의 역활을 한다는 것이다. 이것을 확장해보면 다층 퍼셉트론을 활용하여 다양한 문제를 해결할수 있다는 추측을 할 수 있게 된다.
3. 신경망(Neural Network)
신경망은 퍼셉트론와 동일한 형태를 가진다. 일반적으로 입력층, 은닉층, 출력층 이렇게 3개로 노드를 분류한다.

그러면 신경망과 퍼셉트론의 차이점이 무엇인가라고 생각해본다면 신경망은 활성화함수를 사용한다.
기존의 퍼셉트론은 나온값이 기준치에 따라 0,1중 하나의 값(계단함수라고 부른다)을 사용했다면 신경망은 더양한 활성화함수를 사용한다.
4. 시그모이드 함수(Sigmoid function)
$h(x)=\frac{1}{1+exp(-x)}$

시그모이드 함수를 사용하는경우, 기존 계단함수와 달리 입력에 따라 출력이 연속적으로 변화하고 항상 출력이 0과 1 사이의 값이다. 이러한 시그모이드 함수를 활성화 함수로 사용하게 되면, 기존의 신경망안의 은닉층에서 값들이 버려지지 않고, 신경망이 알수 있도록 연속적인 값들을 반환해준다는 점에서 이점이 있는 것이다!
5. 손실 함수(loss function)
그러면 이러한 신경망을 어떻게 개선할 것인가?(인공지능에서는 학습이라고 한다) 개선하기 위해서는 나온 결과가 옳바른 판단을 했는지에 관한 판단기준이 필요하다. 우리는 원래의 정답과 예측한 값을 손실함수를 정의하여 손실함수를 최소화하도록 가중치의 값을 조정할 생각이다. 손실함수는 다양한 방식으로 측정되는데, 우리는 binary cross entropy을 손실함수로 사용한다. cross entropy은 다음과 같이 정의한다.
$D(S,L)=- \sum_{}^{i}L_ilog(S_i)$
(binary cross entropy를 사용하는 경우 분류기준이 2개 이상인 Multinomial Classification 문제를 해결하지 못함)
6. 소프트 맥스 함수(softmax function)
$S(y_i)=\frac{e^{y_i}}{ \sum_{}^{j}e^{y_i} }$
분류 문제에 활용되는 활성화 함수이다. 예를 들면 10개의 종류를 분류하는 문제를 생각해보자. 이경우 신경망의 출력층이 10개의 노드로 되어있는데 이때 노드의 값이 클수록 해당 인덱스가 정답일 확률이 높아지게 되는것이다. 이때 확률로 표현하기 위해 모든 출력층 노드의 합을 1로 하기 위해 사용한다.(데이터의 일반화라고 할 수 있겠다.)
7. 비선형문제 ->선형문제
SVM에서 커널트릭으로 비선형 문제를 선형문제로 바꾼것과 동일하게 결국 신경망도 선형문제로 바꿀 수 있다.
8 역전파 알고리즘
$x_{i+1}=x_i-\gamma _i \bigtriangledown f(x_i)$
경사하강법으로 가중치값을 조정해나가는데 이때 만약에 신경망의 은닉층이 매우 많다고 가정해보자
합성함수의 미분법을 생각해보면 $y=f(g(x))$의 형태의 합성함수를 미분하면 $y'=f'(g(x))g'(x)$이다.
따라서 은닉층의 개수가 4개만 있더라도 미분식 $y=f(g_1(g_2(g_3(g_4(x)))))$으로 미분하게 되면 미분의 미분의 미분을 하게된다.... 계산량이 늘어나고 우리가 기억해야하는 변수의 개수도 많아진다.
그러나 역전파 알고리즘을 사용하면 backward를 하면서 앞 노드의 미분값과 가중치 weight와 연산의 형태만 알고 있으면 계속해서 미분을 할 수 있어 효율적이다.
역전파 알고리즘의 자세한 설명은 생략하겠다.
'AI > 기계학습' 카테고리의 다른 글
| [기계학습] CNN(Convolutional Network) (1) | 2023.12.09 |
|---|---|
| [기계학습] Artificial Neural Network 2 (0) | 2023.12.03 |
